Составлена математическая модель распространения коронавируса

Обновлено: 24.04.2024

Какие прогнозы по распространению COVID-19 в России делают аналитики

Сбербанк предписал коронавирусу позитивный сценарий для России. По просьбе “Ъ FM” специалисты банка объяснили, как работает их математическая модель распространения эпидемии. Накануне о ней рассказал президент банка Герман Греф. Для России, по его словам, ситуация выглядит неплохо при всех возможных сценариях. Что это означает? И насколько точны прогнозы аналитиков? Об этом — Иван Корякин.

Как коронавирус отразится на деятельности компаний

Все эти параметры специалисты Сбербанка сопоставили с уже собранной статистикой по коронавирусу за несколько месяцев. И подогнали таким образом, чтобы количество авиаперелетов и другие факторы по дням коррелировались, например, с числом заболевших. И уже на основании этого сделали прогноз. А доцент Сколтеха Георгий Базыкин добавил к этой формуле еще и меры борьбы с коронавирусом, которые принимают в Китае. И оказалось, что эпидемия там идет на спад.

«Самая базовая модель построена на основном параметре — числе инфицированных на одного уже существующего инфицированного. Карантин, ограничение передвижений, мытье рук и так далее вот это самое число снижают.

Как опасения по поводу коронавируса снижают мировой экономический рост

Сбербанк также учитывает сезонный фактор — там полагают, что летом коронавирус будет распространяться медленнее. Просто потому, что в теплое время года люди реже болеют респираторными инфекциями. Зато осенью может начаться вторая волна коронавируса. И сложно сказать, затронет ли она Россию, когда в стране первая-то еще не началась.

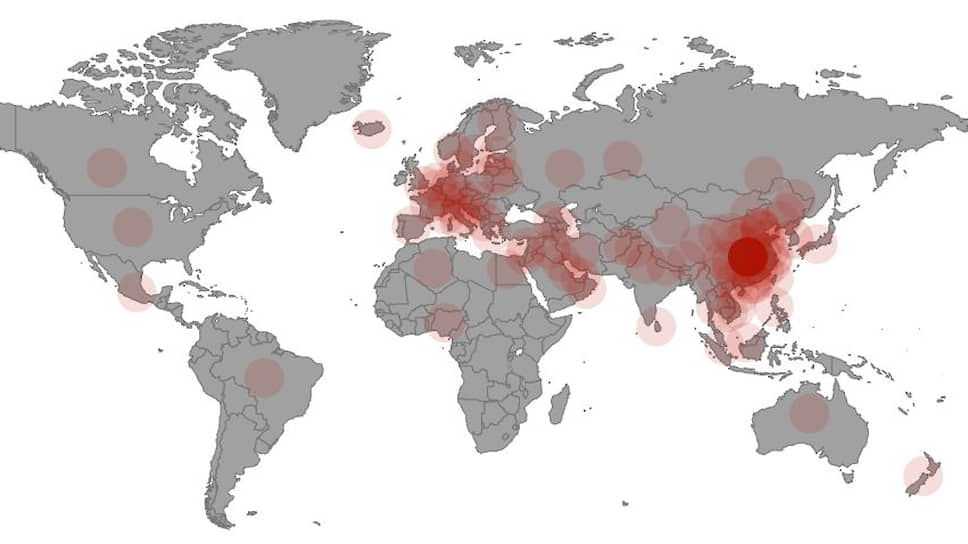
Коронавирус-2020 в Китае и мире

Мэрия подготовила план мер по борьбе с коронавирусом в городе, с ним ознакомились СМИ. Он включает три сценария, в том числе и режим ЧС, который предусматривает закрытие всех предприятий города кроме ответственных за жизнеобеспечение и экстренных служб.

Данная статья написана в 20-х числах марта 2020 г. в разгар пандемии короновируса COVID-19, когда ее итоги в России и в других странах еще не были понятны. На примере исследования простой математической модели показаны возможные сценарии распространения пандемии в зависимости от мер государства, направленных на борьбу с ней.

Ключевые слова: единица времени, математическое моделирование, математическая модель, изоклина бесконечности, изоклина нуля, четверть поля, число заражений, константа, модель, число.

Введение

В государстве в единицу времени осуществляется множество случаев вирусного заражения и осуществляется государственная борьба с пандемией путем проведения множества антивирусных актов. Можно рассмотреть не число антивирусных мероприятий, а количество ресурсов (например, денег) выделяемых государством на борьбу с пандемией, при этом как модель, так и вытекающие из нее выводы не меняются.

Обозначения.

С — число новых заражений в единицу времени.

Р — число антивирусных мероприятий, проводимых государством.

Скорость роста числа новых заражений за единицу времени пропорциональна числу уже зараженных и числу антивирусных государственных мероприятий.

В терминах математической модели

Скорость увеличения или уменьшения числа антивирусных мероприятий, проводимых государством пропорциональна общей численности зараженных и темпу ее изменения.

В терминах математической модели:

В уравнениях a, b, d, e — положительные константы. F₁, F₂, F₃, F₄ — непрерывные функции.

Подробно будем рассматривать случай F₁ (С)=С, F₂ (Р)=P, F₃ (C)=C, .

Система обыкновенных дифференциальных уравнений будет иметь вид:

(1)

Где a, b, d, e = const≥0.

Систему уравнений (1) удобно исследовать в плоскости переменных Р и С сведя ее к одному уравнению:

(2)

Уравнение (2) имеет особую точку С=0, Р=0.

(3) Изоклина 0:

(4) Изоклина ∞:

Утверждение 1. Для первой четверти поля интегральных кривых С, Р изоклина нуля (3) лежит выше изоклины (∞) так как для любых положительных величин

Заметим, что точки, соответствующие началу снижения числа заражений в единицу времени, лежит на изоклине 0 (3).

Собственные значения системы (1) являются решением уравнения:

(5) , где

Получаем в зависимости от знака D три случая.

1. D 0 - различные вещественные, положительные. Особая точка С=0, Р=0 — узел.

В этом случае сепаратриса узла имеет вид:

Утверждение 2. В случае a 0) лежит ниже изоклин 0 (3) и ∞ (4).

Картина интегральных кривых имеет вид:

Рис.2. 1 — сепаратриса узла, 2 — изоклина нуля, 3 — изоклина бесконечности

Из рисунка видно, что при любых начальных данных система приходит в точку (0,0). Нулевой уровень новых заражений и нулевые затраты государства. Однако если государство выделяет недостаточно ресурсов на первом этапе, то на число заражений, все-таки сначала будет расти. Это случай инфекций с невысокой скоростью распространения (константа а из системы (1)).

Утверждение 3. В случае a>be сепаратриса узла в первой четверти поля интегральных кривых С, Р (для С, P > 0) лежит выше изоклин 0 (3) и ∞ (4) Картина интегральных кривых имеет вид:

Рис.3.1 — сепаратриса узла, 2 — изоклина нуля, 3 — изоклина бесконечности

Отметим, что при a=be значение D из (5) меньше нуля и особая точка — фокус. Мы подробно не рассматриваем этот случай, так как он имеет чисто математический интерес.

3. D=0 =(be-a)/2, особая точка С=0, Р=0 — вырожденный узел. Все утверждения и выводы из предыдущего случая имеют место.

Выводы

Заключение

Основываясь на методологии математического моделирования применительно к проблематике распространения вирусной инфекции удается изучить различные сценарии заражения населения в зависимости от действий государства. При исследовании учитывалась зависимость скорости распространения инфекции от общего числа инфицированных в стране, активности государства по борьбе с пандемией. Мы не учитываем число выздоровевших, так как до сих пор точно не известно, приобретают ли они иммунитет, зависимость распространения вируса от природных условий, уровень сознательности населения и т. д. Все уточнения можно ввести в модель, однако, на основных выводах они не отразятся.

Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры.. — ISBN: 5–9221–0120-X. — М.: Физматлит, 2002. — 320 с.
Михайлов А. П., Шамрай А. А. Численное моделирование некоторых одномерных автомодельных течений идеального газа // Математическое моделирование. — 1998. — № 10:6. — С. 31–41.
А. П. Михайлов, В. В. Степанова, А. А. Шамрай. Существование и свойства автомодельных решений задачи коши для уравнений газовой динамики // Журнал вычислительной математики и математической физики. — 1996. — № 36:3. — С. 52–65.

Основные термины (генерируются автоматически): единица времени, государство, изоклина нуля, изоклина бесконечности, константа, математическая модель, модель, четверть поля, число, число заражений.

Вакцины от коронавируса 2019-nCoV нет до сих пор, как нет официальных прогнозов от ВОЗ о перспективах распространения этой заразы по странам. На этом фоне приходится принимать во внимание любые модели поведения коронавируса, хоть как-то описывающие его распространение, которые появляются на просторах интернета. Проверить степень их научности не представляется возможным, тем более что официальным властям особого доверия также нет. Ведь уже известно, что чиновники Китая до 20 января активно скрывали размер эпидемии, и даже не предпринимали никаких мер по её сдерживанию.

В тоже время и турбизнес, и туристы должны строит свои планы хотя бы на каких-то прогнозах. Поэтому приходится рассматривать любые из появляющихся в интернете.

Итак, приводим прогноз по дням (сама модель была опубликована 27 января, и до 30.01 - момента подготовки материала, её прогнозы совпадали с официальными данными о числе зараженных):

Согласно этой модели, если к этой дате путешествия между всеми странами не будут прекращены, а границы не закроются, эпидемия ускорится.

По прогнозам данной модели, если к этой дате путешествия между всеми странами не будут прекращены, а границы не закроются, эпидемия ещё ускорится.

5 февраля, 00:00 GMT:
число инфицированных – 139’000-226’500, находящихся на разных стадиях инкубации (от 1 до 14 дней). Симптомы заболевания у 1’790-1’900.

Модель утверждает, что с этой даты пандемия больше не может сдерживаться без полного карантина, по крайней мере, для всех крупных городов по всему миру. Это будет сопровождаться полным экономическим крахом и паникой.

Читайте другие важные материалы о пандемии нового коронавируса:

➔ Если вы собирались в Китай, то тепрь эту поездку придется отложить на неопределенное время. Однако от путешествий отказываться не стоит - на Земле полно интересных мест. А чтобы вам было проще найти такой маршрут, мы подобрали для вас несколько интересных материалов с ФОТО, которые помогают найти вдохновение для новых путешествий:

(фото) (фото) (фото) (фото) (фото) (фото) (фото) (фото) (фото) (фото) (фото)

В связи с пандемией COVID-19 по сети бродит масса довольно наивных концепций о моделировании эпидемий. Попробуем разобраться. Мы только рассмотрим математические методы моделирования заразных болезней, касаясь медицины и биологии лишь когда требуется прикинуть какой-нибудь параметр.

Экспонента или сигмоида?

Простейшее рассуждение – распространение вируса по экспоненте. Классическая математика из программы средней школы: геометрическая прогрессия, задачка о рисе на шахматной доске, и тому подобное. Пусть каждый инфицированный каждый день заражает, например, r_exp=2 человек. В нулевой день, один инфицированный: бабушка с рынка. В первый день, три инфицированных: бабушка, внук и внучка (внук плюс внучка – это 2, то есть r_exp). Помним, что смертей и вообще симптомов наш вирус не вызывает, оттого ни бабушка, ни внуки, ни окружающие не знают, что у них вирус. Во второй день, девять инфицированных: бабушка, её внуки, родители внуков, четыре одноклассника внуков в школе. Ну и так далее. На 21-й день число заражённых превысит всё население Земли: (r_exp+1)²¹ = 3²¹ = 10.5 млрд.

Ясно, что геометрическая прогрессия неплохо работает в начальном периоде распространения вируса, но затем начинает выдавать сильно завышенные результаты. Мы попробуем решить задачку не в лоб, а правильно. Как её решают в университетах, а не в школах.

Прирост числа инфицированных I (infected) от времени записывается обыкновенным дифференциальным уравнением:

Достаточно проверить решение прямой подстановкой выражений , в уравнение .

Тождество левой и правой частей очевидно при любом t₀. Точка t₀ – это точка максимума функции Хабберта, её мы будем подбирать из граничных условий. Мы знаем, что в нулевой день t=0 инфицирована только старушка с рынка. Значит,

Максимум заразившихся будет на 23-й день. По формуле , в эти критические сутки заразится:

Последний не заразившийся (вообразим такого охотника-одиночку из племени Умба-Юмба) будет на 2t₀, то есть в нашем случае примерно на 46-й день распространения вируса по планете. Доказываем аналитически:

Каждый может проверить, что функция Хабберта – симметрична относительно точки t₀. Теперь нарисуем два графика: нашу сигмоиду и экспоненту. Легко обнаружить, что первые несколько дней экспонента и сигмоида близки. Если I много меньше P, то:

Экспонента у нас была с параметром r_exp= 2, для сравнения положим r = ln(2+1) ≈ 1.1. Тогда t₀ = ln(7.8·10⁹)/1.1 ≈ 20.7.

В конце периода распространения вируса экспонента не работает по определению; там миллиарды триллионов не существующих заражённых. Сигмоида может работает примерно до момента, когда осталось несколько тысяч незаразных. Всех до последнего человека вам не заразить, даже если очень стараться. Полковник Пупкин! Оставайтесь в бункере!

Вообще мы не знаем вирусов, способных заразить всё население планеты за месяц-два.

Во-первых, если такие и были, то проявить свою сущность могли лишь примерно с середины XX века, когда стал общедоступным авиатранспорт. До этого, к племени Умба-Юмба надо плыть месяц на пароходе, потом ехать на слонах по джунглям две-три недели. Приехали заражать последнего, а племя говорит: наш одинокий охотник ушёл! То ли на север, то ли вверх по Замбези.

Полагая, что вирус скрытный, и человек против него никаких мер не принимает, прикинем, очень грубо, реалистические значения r для случая, если заражённые всю жизнь заразны. Пусть вирус втихаря захватывает планету за два года, то есть t₀=365. Из формулы : r = ln(7.8·10⁹) / 365 = 0.06. Если распространение вируса началось, скажем, 1 января, то первый миллион заражённых будет во второй половине августа, а первый миллиард (заметим ещё раз, они не знают, что заражены, симптомов нет) – в конце сентября того же года. Последний миллион не заражённых останется в июле следующего года.

Конечно, с реальными вирусами всё происходит куда медленнее. Не пугайтесь! Сейчас попробуем сделать наш учебно-тренировочный вирус чуть более реалистическим. Дырочку в стволе оставим.

Базовое репродукционное число.

По данным ВОЗ [1], инкубационный период COVID-19 – от 1 до 14 дней, в среднем 5-6. У нашего учебно-тренировочного вируса сделаем такой же. Примерно три недели после инфицирования человек становится не заразен.

Кривая работает так. Если, скажем, 31 декабря 1000 человек заразилось вирусом, то 1 января заразных среди них нет. К 5 января примерно 300 будут заразными, а 700 – пока нет. Восьмого января примерно 900 заразных. На 21 день заразных среди этой тысячи будет около 20. На 30-й день заразных нет.

Конечно, раз на раз не приходится. У всех возбудителей свои кривые. Кривая выше – просто одна из бесконечного множества вариантов. Числовой пример. Я искал, но не нашёл реальных данных по COVID-19; статьи пока не опубликованы. По всем параметрам моя кривая удовлетворяет отчёту ВОЗ [1], но там только опорные циферки, без картинок.

Уравнение теперь записывается как система:

Здесь C(t) – количество заразных (contagious), S(t) – количество людей, которые могут заразиться вирусом (susceptible).

Переменное репродукционное число. Дистанцирование.

В Интернете модно выдавать страждущим примерно вот такие советы (писано вроде 13 марта):

Поглядим на формулу . Интеграл заразности зависит в основном от биологии вируса и биологии человека; он примерно постоянен. А вот трансмиссивность r зависит от:

Скорости воспроизводства вируса в организме больных. Скажем, COVID-19 быстрее размножается (поражает больше клеток в единицу времени) у людей пожилых.

Способа распространения вируса. Скажем, COVID-19 распространяется в основном воздушно-капельным путём.

Устойчивости вируса во внешней среде.

Погодных условий. Например, при сильной инсоляции вылетевший наружу коронавирус остаётся опасным считанные секунды. Ультрафиолет корёжит РНК.

Социальных привычек населения. Принято ли у вас мыть руки после уборной?

Местного этикета. Принято ли в вашей стране целоваться при знакомстве или можно пожать руку? А целоваться со знакомыми при каждой встрече?

Вида занятости населения. Офисы или шахты? А может, ювелирные мастерские? Сколько человек трудится вместе? Есть ли профессиональные лёгочные заболевания?

Может ли заболевание передаваться животными? Насекомыми? В какое время года они активны?

Если спросите у квалифицированного эпидемиолога, он в этот список накидает ещё пару сотен пунктов.

Разные значения R₀ могут быть даже в одном городе, но в разных слоях общества. Торговцы с рынка в Ухане имеют немного другие гигиенические привычки и условия труда, чем программист или разработчик печатных плат из того же индустриального мегаполиса. То, что в Китае в среднем получилось 2.0-2.5, совсем не значит, что в среднем по миру будет 2.3. Может быть и больше, и меньше.

Если у болезни появляются какие-то неприятные симптомы, в дело вступает дистанцирование (distancing), начинающее давить R до значений существенно меньше R₀.

Если человек весь фиолетовый, он вызывает закономерное любопытство. Очень быстро, дней через 5-7, люди замечают, что почти всякий, кто близко с фиолетовыми пообщался, сам становится фиолетовым. Хотя болезнь довольно быстро проходит, и никто не умирает, население быстро сделает определённые выводы, и фиолетовых будут сторониться. При том, сами фиолетовые не будут лишний раз контактировать со здоровыми, стесняясь симптомов заболевания (ну и не желая заражать других). Это и есть дистанцирование.

Незнание микробиологии не помеха. Люди сделали достаточно достоверные выводы про лёгочную форму чумы, туберкулёз и сифилис, не зная ни микроскопа и генетики, ни вообще о бактериях и вирусах. Даже для болезней с огромным инкубационным периодом, типа лепры, во многих обществах было чёткое понимание, что лишний раз с больным лучше не контактировать, а после контакта надо руки помыть. И раздавали прокажённым одновременно и милостыню, и колокольчики.

Для численного примера пока предположим, что для вирусоносителя без симптомов остаётся параметр R_N=R₀, а для явно заболевших – он вдвое ниже, R_S=R₀/2. При этом, ни о какой изоляции заболевших речи нет. Заболев, фиолетовые просто уменьшают количество своих дневных контактов в среднем вдвое: на улицу выходят реже, на работу не ходят, сидят по домам. Выше мы уже договорились, что на 30-й день переболевший полностью не заразен, значит, после исчезновения фиолетовой сыпи может безопасно вернуться в общество. Система уравнений переписывается так:

Здесь M(t) – количество явных больных. C_S(t) и C_N(t) – число вирусоносителей с симптомами и вирусоносителей без симптомов, соответственно.

Выбранное нами социальное (применяемое населением добровольно, без армии, полиции, законов, и т.п.) дистанцирование с R_S= 2.30/2 = 1.15 – это даже не полумера; эпидемию тормозит, но не останавливает. А мы такое значение тут специально; если поставить R_s вблизи 1, то миллиардов заражённых никак не получится, график превратится в прямую линию!

Читайте также: